Some Ruminations on the Configuration of the Yavin/Yavin IV System
(Warning: Headbanger Page)
Summary:
Yavin IV probably orbits Yavin at about 500,000 km radius, which is close enough to have
Yavin cover apparently 22° of its sky.The red gas giant planet Yavin is actually a
"brown dwarf", radiating cozy infrared radiation which is Yavin IV's main heat source.
The sun, while it illuminates Yavin IV nicely, is a minor source of heat. Yavin IV
turns about its axis once every 24 standard hours (1 ) and completes
one orbit around the gas giant Yavin in about 12 ¼ hours.
Determining the Size of Yavin IV's Orbit and Its Distance From Yavin
One of the basic things we need to determine, before saying what Yavin IV's
day-to-day sky looks like, is where exactly Yavin and Yavin IV are located
with respect to one another. Their relative distances will determine how
big in the sky Yavin looks, for example. The relative distance question
looks like an easy one to answer, but as we see, it's not so trivial!
Well, you say, we already know how big Yavin looks from Yavin IV! Ralph McQuarrie's
concept painting of the X-Wing launch, and the scene in A New Hope which
is derived from it, show the red planet Yavin taking up a very goodly portion
of the sky. Although we see only a sliver of the actual planet, its curvature
implies that it takes up anything from 22 degrees to 50 degrees of sky arc
(for reference, our moon takes up 1/2 degree of sky arc). (We consider horizon-to-horizon
to be 180 degrees.) This apparent size
is determined by/will determine Yavin IV's orbital radius, as indicated below.
West End Games' Galaxy Guide 2: Yavin and Bespin
(1 ) states that the gas giant Yavin is 192,478 km in diameter, or 96,239
km in radius, which is what we use here.
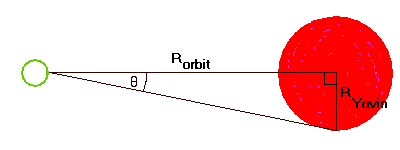
This figure shows that the radius of Yavin IV's orbit, and the radius of the planet Yavin
perpendicular to this line, form a right triangle which sweeps out an angle, the
'apparent angular width' of half of Yavin, as seen from Yavin IV. The ratio of these
lengths forms the tangent of angle Theta. Just multiply theta by 2, to get Yavin's
full "angular width" in the sky.
| r | Theta | Yavin covers: |
| 7 million km | 0.78 degrees | 1.56 degrees |
| 3 million km | 1.84 degrees | 3.68 degrees |
| 1 million km | 5.5 degrees | 11.0 degrees |
| 500,000 km | 10.9 degrees | 21.8 degrees |
| 250,000 km | 21 degrees | 42 degrees |
| 206,301 km | 25 degrees | 50 degrees |
| 96,200 (impossible) | 45 degrees | 90 degrees |
In the shot where the Millenium Falcon curves round Yavin to get to Yavin IV, the
moon (Yavin IV is technically a moon) appears to be pretty close to the planet. This jibes
with the above table; altogether the visuals we saw in the movie imply that Yavin IV
orbits at a radius of some 200,000-500,000 km out from the center of the gas giant Yavin.
Here we immediately hit a problem with West End Games' data. The WEG GG2 states that Yavin IV
orbits Yavin roughly 3 times "in a standard year" (which we can take as being equivalent to
a Terran, or Earth year). This gives us an orbital period of some 4 months for the
moon. We toss Kepler's Third Law at the question, to determine Yavin IV's orbital
radius from this:
|
T² = 4 x PI² x (r³)/(G x M) |
(2 ) |
where:
T = period (time to complete one orbit)
r = radius at which our body is orbiting the big body
M = mass of the big body (in our case mass of gas giant Yavin)
G = Newtonian constant of gravitation, 6.670e-11 m²/kg-s²
The WEG GG2 states that Yavin's mass is 323.7 x the "Galactic standard" for
humanoid-habitable planets-- if this is 323.7x mass of Earth, then Yavin weighs 1.93e27 kg.
This is pretty close to the size of Jupiter, which weighs 1.9e27 kg. (3)
Translate 4 months into seconds, and solve for r (radius of the orbit) which comes out in
meters... translate it back into kilometers, and we get-- 7 million km?? This clearly cannot be
correct, as at that range (see table above), Yavin would look only 3 times as big as our
own moon! So, where the West End Games' data and the movie's data differ, we have to toss
WEG out and go with what we saw in the movie. Leaving us with an orbital radius of
200,000-500,000 km.
As those of us who follow space probes know, the moon Io, Jupiter's closest Galilean (big)
satellite, is pretty tectonic. This tectonism is thought to be caused by heat induced from
tidal stresses, which in turn come from the moon being so close to Jupiter. Io orbits
Jupiter at 421,600 km (3 ). In the fictional accounts of Yavin IV
(The Jedi Academy trilogy by Kevin J. Anderson; and some of the
Dark Horse comics),
tectonic activity or volcanism is not really mentioned, although the WEG GG2 does state that Yavin IV has "fairly strong tectonic
action that lets heat escape from the very depths of the satellite."
(1 )(p.13). So we can probably assume some but not a tremendous amount of
volcanism... which means we prefer to put Yavin IV about 500,000 km out so as not to tear
it up too bad, but also have Yavin hanging large in the sky as portrayed.
So How Does Jedi Master Luke Skywalker Stay Warm?
A different question now raises its head. The WEG GG2 states that Yavin orbits its sun in a period of
about 13 years... this is similar to Jupiter's period of 11.86 years(3 ). At
this range, these celestial bodies do not get a lot of sunlight. In fact, due to the inverse-square
law of radiation
(E = I/d²)((2 )p.383)
all other things being equal,
the amount of energy E received per area decreases with the inverse square of the distance d.
In other words, a planet twice as far away gets only ¼ as much sunlight.
We know that Earth, on the average, receives about 1370 W/m² from the sun .
Since Jupiter, whose distance we will use for this, is ~5x as far from the sun as Earth, it gets 1/d²
or 1/25 as much sunlight as we do ---> 54.8W/m². (5 ) This is not enough
to keep the flagstones warm in the Massassi courtyard.
So, being that we have our planetary system so far from the sun so the gas giant won't blow away, and we
want to keep Yavin IV from being torn apart by tectonics, how are we supposed to heat it warm enough to
be a tropical jungle Earthlike world? Here, our butts get saved by a neat little phenomenon called the
Kelvin-Helmholtz mechanism. (6 ) And if you can find an equation for
this puppy, let me know where, because I'd like to see it. To sum up, the Kelvin-Helmholtz mechanism
says that "if you have a big heavy gas planet, it squashes down on its own center so hard that it actually
generates heat." As a result of this, Jupiter's core temperature is estimated at 20,000K and its mean
cloud temperature is -121°C or 152K, which is warmer than we'd expect for its distance from the
sun.(6 )
So, OK, great, our Jupiter-sized gas giant Yavin might be marginally warmer than the liquid nitrogen in the
chemistry department's vacuum flask. How exactly is this supposed to keep Yavin IV warm? At this point, we
commence to explore the black-body properties of Yavin, to determine just how warm this gas giant
would have to be.
We'll use several equations. Stefan-Boltzmann's Law:
E = 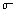 x T^4 x T^4 |
|
with:
E = energy output in W/m² where m² is the surface area of the body;
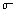 = the Stefan-Boltzmann Constant, 5.57e-8 W/m² K^4
= the Stefan-Boltzmann Constant, 5.57e-8 W/m² K^4
T = the temperature in Kelvin K.
An equation for Calculation of Solar Constants:
|
Flux = Total Power/Area At the Radius |
|
The "Flux" is the energy/unit area, or the W/m² seen above,
and "Total Power" comes from the body's energy emitted.
"Area at the Radius" is the surface area of a sphere calculated at the radius r where we
want to know what the energy flux is. Note that "energy flux", and "solar constant," are the same
thing when we are looking at how much sunlight energy passes through a certain area.
The Body's Total Power Emitted comes from
Power = 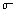 x T^4 x (surface area of body) x T^4 x (surface area of body) |
|
with T = temperature in Kelvin K and
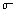 the same constant as above;
the same constant as above;
And, of course, the Surface Area of a Sphere is
We can use this one both for the surface area of Yavin, and for the area of the region of space at radius
'r' out from Yavin's center, i.e. at the location of Yavin IV.
We know that we want to keep Yavin IV as warm as Earth, and Earth receives 1370 W/m². Jupiter
receives 54.8 W/m² of sunlight, which is probably about what Yavin IV receives. If we assume that
Yavin IV is a little bit more tectonically active than Earth, we can guess it gets about 15 W/m²
from internal heat. This leaves us with needing about 1300 W/m² from Yavin.
We have established that Yavin IV orbits at about 500,000 km from Yavin. So now, we can calculate the
total energy that Yavin has to emit, in order to give Yavin IV an energy flux of 1300 W/m² at this
distance. We use the Solar Constant equation above, solving for Total Power.
With the distance r converted to meters, we get 4.084e21 W emitted out of Yavin at large. (Meaning
4.084 x 10^21 watts)
We plug in Yavin's radius to the Surface Area of a Sphere to get Yavin's surface area.
Then we put this back into the Solar Constant equation, this time solving for E, the energy flux
coming off Yavin's surface. We get 35090 W/m².
And using the Stefan-Boltzmann equation, this gives us a surface temperature for Yavin
of 890 K. Remember that Jupiter's temperature is 152 K! Water boils at 373 K, so Yavin's surface would
be pretty toasty. Is this possible?
Let us consider the humble brown dwarf.
A brown dwarf is simply a Jovian-style planet that was almost, but not quite massive enough to start
nuclear fusion and become a star. They still generate plenty of internal heat due to the
Kelvin-Helmholtz mechanism, and in fact are theorized to start out at surface temps as high as 3000 K,
gradually cooling to 300K after, oh, 10 billion years or so. One of these could be still 800 or 900 K
after a billion years, which could be long enough for life on Yavin IV to evolve into a jungle. In fact,
it might stay in that temperature range for several billion years...
Also, in size (diameter), a brown dwarf can be quite close to that of Jupiter. In fact the known brown dwarf
Gliese 229B is about Jupiter's size, and has an estimated surface temperature of 900 K. Perfect!
All these brown dwarf facts are (9 ).
What sort of radiation is the ruddy "brown" dwarf Yavin emitting? We can consider the following
diagrams:
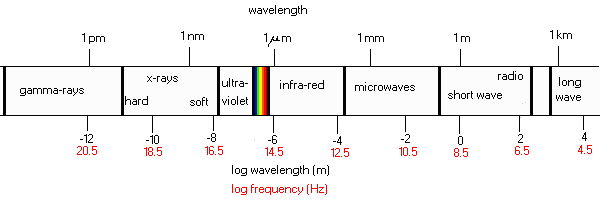
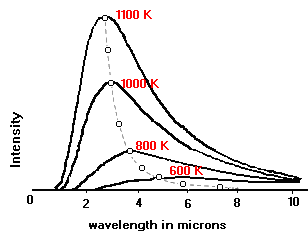 (10 )
(10 )
The bottom diagram is derived from the Wien's Displacement Formula:
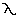 max emittance = 2897 / T max emittance = 2897 / T |
|
with 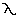 max emittance being the wavelength of peak energy emission (in
µm) at temperature T (in Kelvin).
max emittance being the wavelength of peak energy emission (in
µm) at temperature T (in Kelvin).
And when we do the math we find that indeed Yavin at 890 K would have its peak energy emission at about
3.25 µm, which is in the near infrared (see figure above).
Thus Yavin is not only a red gas giant planet, it is an infrared gas giant.
How well lit is Yavin IV?
Plug 54.8 W/m², the amount of sunlight Yavin must get at an
orbital radius similar to Jupiter's, into the Solar Constants equation:
|
Flux = Total Power/Area At the Radius |
|
As "Flux", use a 100W light bulb for "Total Power" (=100W) and solve for the radius from
"Area At The Radius", where "Area At the Radius" is the surface area of a sphere:
We find that this amount of solar flux turns out to be
equivalent to the light from a 100W bulb about 1 foot away. So Yavin and Yavin IV are lit a little
better than your living room.
How Quickly Does Yavin IV Orbit Yavin?
We have established above that Yavin IV must orbit Yavin at about 500,000 km out, and that Yavin is
a brown dwarf pretty similar to Gliese 229B. Gliese 229B is estimated to weigh 20x to 50x as much
as Jupiter (11)).
We plug these numbers into the equation for Kepler's Third Law:
|
T² = 4 x PI² x (r³)/(G x M) |
(2 ) |
where:
T = period (time to complete one orbit)
r = radius at which our body is orbiting the big body
M = mass of the big body (in our case mass of gas giant Yavin)
G = Newtonian constant of gravitation, 6.670e-11 m²/kg-s²
Solving for period T, we find that Yavin IV must orbit Yavin in 12 ¼ hours if Yavin weighs 20 times
as much as Jupiter, and the orbital period would be 7.5 hours if Yavin weighed 50x as much. Whee!
We'll choose the more conservative estimate, as we wouldn't want the Jedi students to get vertigo.
Crocuta note: Please feel free to check this math, and if you find any gross mistakes,
PLEASE LET ME KNOW!!
Credits and Sources (This page only)
1) West End Games' Galaxy Guide 2: Yavin and Bespin © 1995
2) Introduction to College Physics, Harvey E. White. © 1969
3) Calvin J. Hamilton's Jupiter Info page
5) Todd Barber's Online From Jupiter
6) Bill Arnett's "Nine Planets: Jupiter"
9) All brown dwarf facts are:
10) Thanks to
Beverly Lynds for the nice EM and
blackbody diagrams, and also for the "sigma" and "lambda" gifs.
11)Brown Dwarf Gliese 229B in Lepus,
CalTech and Johns Hopkins astronomers
 |
 | |
 |
| Back to Crocuta Main |
Back To Docking Bay 94 | |
Back To Yavin IV |

...because WordPad would have been
overkill.

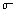 x T^4
x T^4

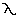 max emittance = 2897 / T
max emittance = 2897 / T 


